I Understand Noise Figure, but How Did Noise Get a ‘Temperature’?
The concept of “noise factor” and “noise figure” is reasonably intuitive: it is the noise which a component such as an amplifier adds to the input signal as the input signal passes through to the output, or is generated by the thermal motion within a passive component. There are many sources of this unavoidable, internally created noise including entropy, device and material physics, random motion of electrons, and various imperfections, to cite a few causes.
The quantitative definition of noise factor (F) is straightforward: it’s the ratio of input signal-to-noise ratio (SNR) to output SNR:
Noise Factor (F) = (Input Signal/Input Noise)/(Output Signal/Output Noise)
Even passive, non-gain components such as resistors have a noise factor, defined as the ratio of the noise produced by a real resistor to the simple thermal noise of an ideal resistor. To standardize the comparison, the noise factor is measured at a standard temperature of 290K, a choice which is largely a consequence of seminal research done by Harald Friis at Bell Telephone Laboratories in the 1930s. The standard noise source used for comparison has a noise level of KT, where K is Boltzmann’s constant (1.38 × 10-23 J/K).
So how does that get us to noise figure (NF)?
It’s a simple relationship: NF (in dB) = 10 × log (F).
Why have both Noise Factor F and Noise Figure NF? It depends on the type of signal path analysis being done. For some types of analysis, F is more useful, while for others, NF simplifies the equations.
But then there’s another “noise” parameter that comes up: Noise Temperature. How can noise have a temperature? Why would you want to relate noise to temperature anyway?
Here’s why: Noise Temperature is another way of characterizing noise magnitude and associated signal-to-noise changes. It is used in RF links, especially those associated with radio astronomy, space-oriented links, and other non-terrestrial systems.
Start with a definition of Noise Temperature (NT):
NT= 290 × (F-1) [The “290” is from the standard reference temperature, as noted above]
So far, Noise Temperature seems like just another way of quantifying noise, but it is much more. It is a theoretical “abstract” that calls out the equivalent temperature which would produce that same amount of noise power as is seen. Keep in mind that this equivalent noise temperature, often designated as TEQ, does NOT indicate the actual temperature of an amplifier as you would measure it with a thermometer.
Why even use noise temperature and TEQ? Again, for some types of analysis, it simplifies the assessment of the signal chain and the associated equations. It also provides a very useful metric related to defining the noise of less tangible sources such as the noise pervading the sky (yes, the sky is a noise source).
In a wireless link, the equivalent input noise temperature TEQ would be the sum of two noise temperatures: the antenna noise temperature TANT at the output of the antenna, and the system noise temperature of the receiver circuitry TSYS:
TEQ = TANT + TSYS
Noise temperatures of the various stages can be linearly added to characterize the noise at any point in the signal chain (Figure 1).
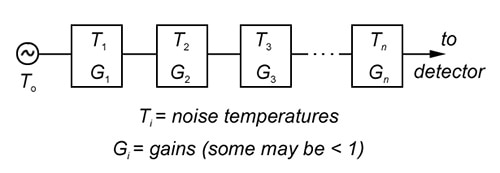 Figure 1: The noise temperatures of individual stages can be added to determine the noise at various points in the system, starting with the equivalent noise temperature at the antenna or other source. (Image source: New Jersey Institute of Technology)
Figure 1: The noise temperatures of individual stages can be added to determine the noise at various points in the system, starting with the equivalent noise temperature at the antenna or other source. (Image source: New Jersey Institute of Technology)
In radio, radar, and space-centric RF systems operating at hundreds of megahertz (MHz) and tens of gigahertz (GHz), the noise at lower frequencies is not an issue as it can easily be filtered and attenuated. Instead, the major sources of noise are background radiation noise as well as internally generated noise. For this reason, any analysis must include these noise sources. If the antenna is pointed towards the sky, the source equivalent input noise temperature, TEQ, depends on the relative position of the sun and its various cycles (see the JPL/NASA paper “Solar Brightness Temperature and Corresponding Antenna Noise Temperature at Microwave Frequencies”).
The study of this “sky noise” led to the discovery of Cosmic Microwave Background Radiation (CMBR) of space and its apparent meaning by Arno Penzias and Robert Wilson (who won the Nobel Prize for this discovery; (see “Cosmic Microwave Background”). Their receiver, comprising a huge horn antenna, recorded an excess 4.2 K antenna temperature almost uniformly pervading space, regardless of antenna orientation (Figure 2). They could not account for this through any circuit and system noise analysis, and finally demonstrated analytically that it was most likely a remnant representing the heat left over from the “Big Bang” as an embodiment of the well-known physics phenomenon of blackbody radiation.
 Figure 2: An image of the cosmic microwave background radiation, taken by the European Space Agency Planck satellite in 2013, shows the small variations across the sky. (Image source: ESA/Planck Collaboration via Space.com)
Figure 2: An image of the cosmic microwave background radiation, taken by the European Space Agency Planck satellite in 2013, shows the small variations across the sky. (Image source: ESA/Planck Collaboration via Space.com)
But don’t be put off by this apparently abstract use of the noise temperature, as the principle of equivalent noise temperature as a noise-related metric has practical, down-to-earth uses (literally and figuratively), in addition to cosmic and space-related analysis. For example, antenna noise temperature is the temperature of a hypothetical resistor at the input of an ideal noise-free receiver that would generate the same output noise power per unit bandwidth as that at the antenna output at a specified frequency.
Noise, of course, is a major issue of concern and challenge in nearly all systems, whether wired or wireless. There’s much more that could and should be discussed, such as bandwidth and its effect on noise power. Noise Factor, Noise Figure, and Noise Temperature are all valid ways to measure noise, and you can easily convert a reading on one scale to another. The “right” one to use depends on the analysis being done and the type of answers desired.

Have questions or comments? Continue the conversation on TechForum, DigiKey's online community and technical resource.
Visit TechForum










