Introducción al procesamiento de señales: Filtro de media móvil

Las señales y los sistemas son conceptos poderosos en ingeniería eléctrica. Nos permiten modelar cómo la información pasa a través de los componentes eléctricos y se modifica. Es más, una vez que comprendemos cómo las señales como los voltajes se ven afectadas por los diferentes componentes eléctricos, podemos diseñar circuitos para manipular las señales de la manera que queramos. Por lo tanto, es fascinante cómo podemos usar una combinación de componentes eléctricos, como resistencias, capacitores y amplificadores operacionales (optoamplificadores), para diseñar herramientas matemáticas como la integración y la diferenciación.

Por ejemplo, eche un vistazo al siguiente circuito (Figura 1):

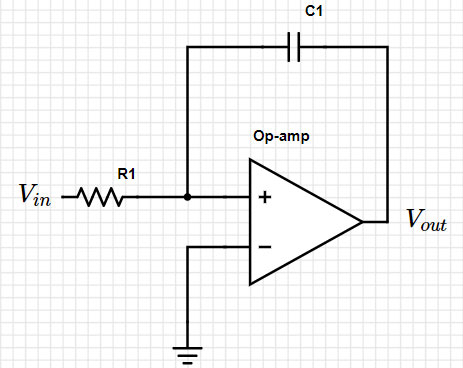Figura 1: Circuito integrador simple. (Fuente de la imagen: Mustahsin Zarif)

Pasando al dominio de Laplace, podemos representar el circuito con la fórmula:

Vout = -(1/s) (1/RC) Vin

¡1/s en el dominio de Laplace corresponde realmente a la integración! Por lo tanto, tenemos un modelo de circuito para un circuito integrador que utiliza un amplificador operacional. Sin embargo, cuando recurrimos al mundo real, los sistemas siempre están contaminados con algún tipo de ruido aleatorio.

Al poner el circuito integrador en espera para un ejemplo más simple, considere un circuito amplificador de voltaje cuyas formas de onda de entrada y salida se pueden medir con un osciloscopio como la Figura 2.

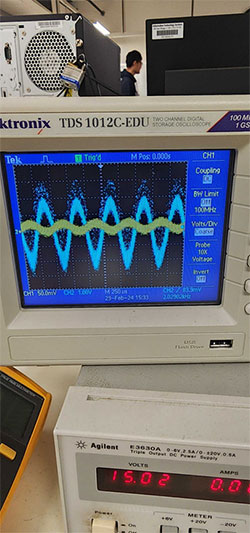Figura 2: Formas de onda de entrada y salida del amplificador de voltaje. (Fuente de la imagen: Mustahsin Zarif)

El ruido aleatorio que se agrega a las formas de onda sinusoidales visibles subyacentes puede deberse a una gran cantidad de factores, como conexiones eléctricas deficientes, ya que el circuito está construido sobre una placa de pruebas. Este ruido también afecta a la forma de onda del integrador, lo que veremos en un futuro blog de esta serie sobre Procesamiento de señales. Sin embargo, lo que a menudo nos interesa es cómo minimizar las perturbaciones aleatorias.

Técnicas de filtrado

A los ingenieros les gusta superar estos obstáculos empleando técnicas de filtrado, que se pueden clasificar como 1) Filtros de respuesta a impulsos finitos (FIR) o 2) Filtros de respuesta a impulsos infinitos (IIR).

Los filtros FIR se llaman así porque la salida en cualquier momento depende solo de los valores actuales y anteriores de la entrada, y no dependen de los valores anteriores de la salida. Por lo tanto, tiene una estructura no recursiva sin retroalimentación que se puede modelar como Ecuación 1.

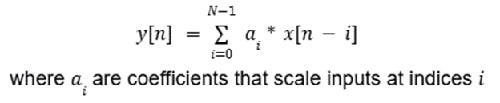Ecuación 1: Ecuación de ejemplo de filtro FIR. (Fuente de la imagen: Mustahsin Zarif)

El circuito integrador es un ejemplo de un filtro FIR, ya que la salida depende únicamente de la entrada.

Los filtros IIR, por otro lado, tienen retroalimentación, ya que la salida en cualquier momento depende de las salidas anteriores, así como de la entrada actual. Esto se modela como Ecuación 2.

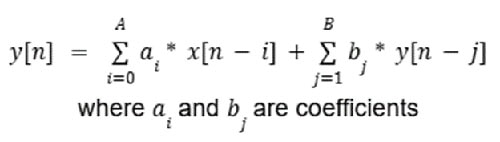Ecuación 2: Ecuación de ejemplo de filtro IIR. (Fuente de la imagen: Mustahsin Zarif)

La Figura 3 es la representación visual del diagrama de bloques de un filtro IIR, que muestra cómo las entradas y salidas se retrasan (z-i, z-j), se escalan (ai, bj) y se suman para obtener la salida actual. Al cambiar estos valores, podemos implementar diferentes tipos de filtros.

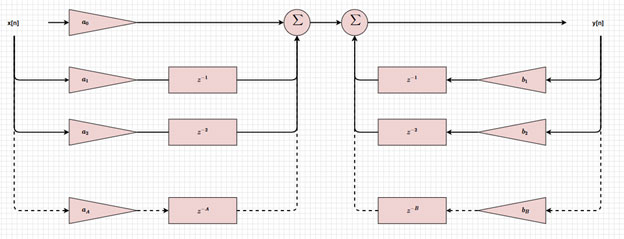Figura 3: Diagrama de bloques de un filtro IIR. (Fuente de la imagen: Mustahsin Zarif)

Si quisiéramos el diagrama de bloques de un filtro FIR que no tiene retroalimentación, y[n] sería simplemente el resultado de la primera suma (Figura 4).

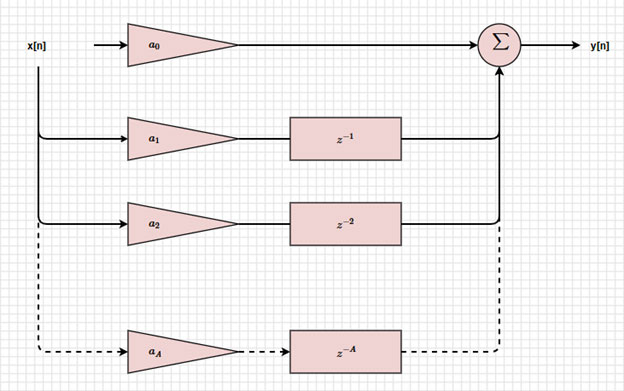Figura 4: Diagrama de bloques de un filtro FIR. (Fuente de la imagen: Mustahsin Zarif)

Ahora que hemos aprendido los conceptos básicos de los filtros FIR e IIR, usemos un ejemplo para ilustrar lo que aprendimos: el filtro de media móvil.

La forma en que funciona la media móvil es tomando el promedio de la entrada actual y un cierto número de entradas anteriores (Ecuación 3).

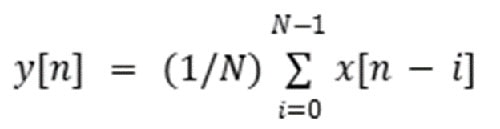Ecuación 3: Ecuación de la media móvil. (Fuente de la imagen: Mustahsin Zarif)

Donde N= tamaño de la ventana/número de muestras que contribuyen a la salida

Podemos ver que se trata de un filtro FIR, ya que no hay términos y en el lado derecho de la ecuación.

Sin embargo, podemos ser inteligentes y reorganizar la ecuación para formar un filtro IIR. Tenga en cuenta lo siguiente:

Si N=5, entonces

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1])/5,

y y[6] = (x[6]+x[5]+x[4]+x[3]+x[2])/5

y[6]=(x[6]+y[5]-x[1])/5

Por lo tanto, la salida actual ahora depende de la salida anterior (y[6] depende de y[5])!

En términos más generales,

y[n] = (y[n − 1] + x[n] − x[n − N - 1])/N

Donde N = tamaño de la ventana

Este filtro funciona de maravilla en el suavizado de las señales en el dominio del tiempo, como se muestra en la Figura 5 que simulé usando python para un tamaño de ventana N = 11.

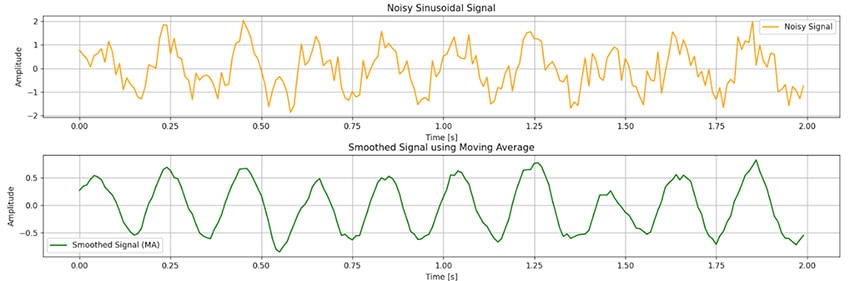Figura 5 : Simulación de filtro móvil usando Python. (Fuente de la imagen: Mustahsin Zarif)

Código Python de simulación de filtro móvil:

Copiarimport numpy as np

import matplotlib.pyplot as plt



# Parameters for the sinusoidal wave

frequency = 5  # in Hertz

sampling_rate = 100  # Sampling rate in samples per second

duration = 2  # in seconds



# Generate time axis

t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)



# Generate a clean sinusoidal signal

clean_signal = np.sin(2  np.pi  frequency * t)



# Add random, white (Gaussian) noise to the signal

noise_amplitude = 0.5

noisy_signal = clean_signal + noise_amplitude * np.random.normal(size=t.shape)



def moving_average(signal, window_size):

    window = np.ones(window_size) / window_size

    return np.convolve(signal, window, mode='same') 



# Apply moving average to the noisy signal

window_size = 11

smoothed_signal_ma = moving_average(noisy_signal, window_size)



# Plot the noisy and smoothed signals

plt.figure(figsize=(12, 9))



plt.subplot(2, 1, 1)

plt.plot(t, noisy_signal, label='Noisy Signal', color='orange')

plt.title('Noisy Sinusoidal Signal')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.subplot(2, 1, 2)

plt.plot(t, smoothed_signal_ma, label='Smoothed Signal (MA)', color='green')

plt.title('Smoothed Signal using Moving Average')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.tight_layout()

plt.show()

Resumen

Comenzamos este blog mostrando cómo, en el mundo real, los datos se corrompen por el ruido. Si bien no podemos obtener la respuesta ideal que esperaríamos de las ecuaciones matemáticas, es posible filtrar las características no deseadas de nuestros datos recopilados para que coincidan con la respuesta ideal lo más cerca posible. Hay múltiples métodos para hacer esto y múltiples escenarios en los que querríamos hacerlo. Si bien terminamos este blog con una respuesta simulada del filtro de media móvil, para el próximo blog veremos cómo el filtro de media móvil exponencial puede suavizar los datos ruidosos de la unidad de medición inercial (IMU).